おはようございます😄

今回は前回の内容の答え合わせをやっていきたいと思います。

前回の内容は下のリンクより

たまには一緒にサイコロでも投げてみましょうか？　Shall we throw the dice together once in a while? | 富山育英センター (toyama-ikuei.com)

正解は④の約2.16回でした🙂

とりあえず、ゴールにたどり着くまでに、サイコロを平均で何回投げることになるか計算で求めてみます。

ここをクリックすると、読み飛ばせます。

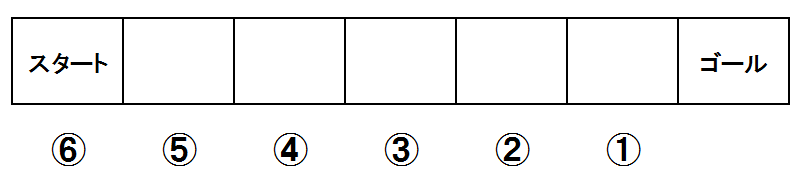
上のように①～⑥までの番号をつけます。

①からスタートしてゴールするまでにサイコロを投げる回数の平均をＥ1とします。

①からスタートした場合、どの目が出ても必ずゴールできるので、ゴールするまでに必要なサイコロを投げる回数の平均値は１です。

つまり　Ｅ1 ＝ １　になります。

問題はここからです！

②からスタートしてゴールするまでに必要なサイコロを投げる回数の平均をＥ2とします。

②からスタートした場合

１の目が出た場合　→　①のマスに一度とまりますので、ゴールするまでにサイコロを投げる回数の平均値は  (Ｅ1+１)  回です。

２～６の目が出た場合　→　そのままゴールしますので、ゴールするまでにサイコロを投げる回数の平均値は１回です。

以上より、Ｅ2 は以下の式から求めることができます。

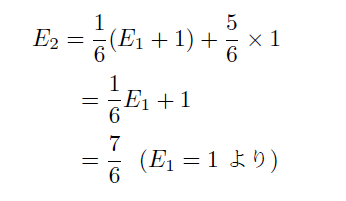
③～⑥からスタートした場合も同様に、サイコロを投げる回数の平均をＥ3～E6 として式を立てると…

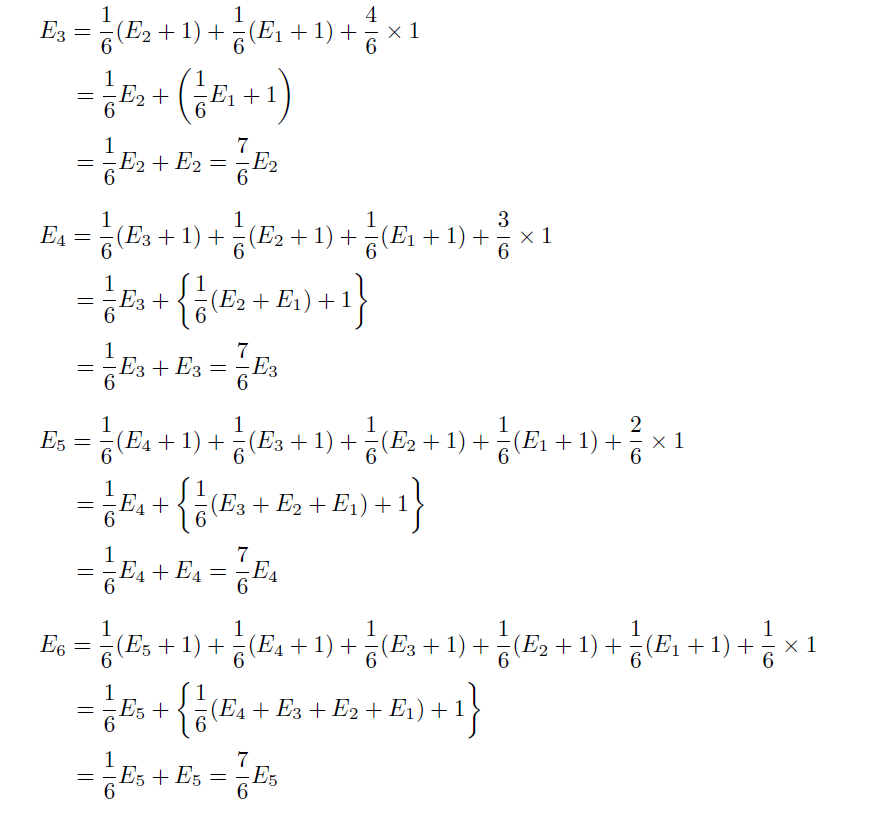
上の式から、今回求めるものは E6 であるので

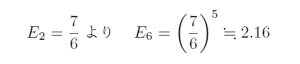
となります。

長かった….

☆☆

『サイコロを２回投げたとき、出る目の和の平均値が７』であることと

『和が７となるまでサイコロを投げるとき、サイコロを投げる回数の平均値』は意味が違いますよね。

サイコロ２回で平均７だからと言って、ゴールまで６マスならばだいたい１回と少しでたどり着ける！

そんなことはないですよ😐

前回の問題を間違えた方、以下の例を見ればすぐに気が付けるはずです。

サイコロ１回投げるとき、出る目の平均値は3.5ですよね。

なら、ゴールまで２マスだった場合は、0.5~0.8回サイコロを投げればゴールまでたどり着けますか？

必ず１回以上はサイコロを投げますよね？