「コッホ雪片」という図形があります。

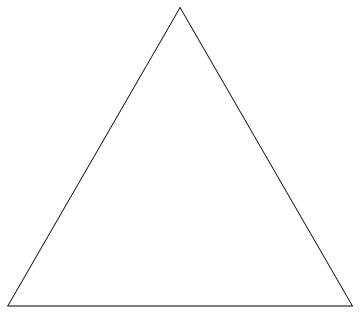
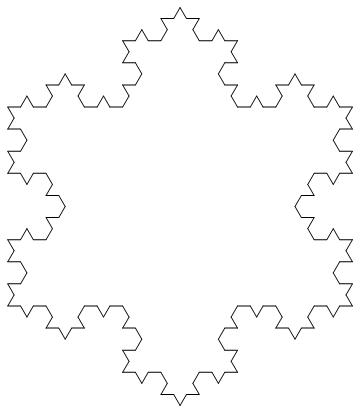
ざっくり言うと、正三角形から始めて、各辺を3等分した真ん中の部分に山を追加していく操作を無限に続けたものです。

フラクタルと呼ばれる図形の1つで、高校の問題集にもよく登場します。

フラクタルとしての性質や特徴も面白いのですが、今回は一旦置いておいて長さや面積に注目してみます。

簡単な計算によりわかりますが、周の長さは無限大に発散し、一方で面積は有限値に収束します（計算してみてください）。

周りの長さはどこまでも長くなるのに面積が一定値に近づくというのはなんとなく不思議ですね。

では、3次元で同じような例を考えてみましょう。

y=1/x の x≧1 の部分を x 軸の周りに回転してできる曲面を「ガブリエルのラッパ」といいます。

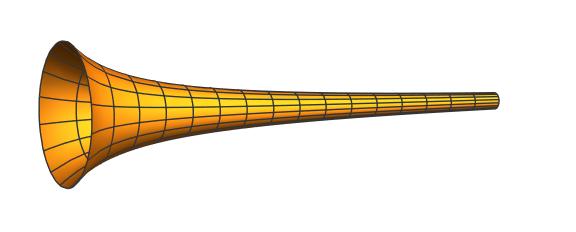
この図形は、表面積は無限大に発散し、一方で体積は有限値に収束します。

因みに、これと逆のことは起こりません。

つまり、表面積が有限なのに体積は無限大に発散する、というような回転体はありません。

ところで、ガブリエルのラッパの形のバケツがあったとしましょう。

このバケツの体積（容積）は有限なので、有限の量のペンキで満たすことができます。

一方、表面積は無限大なので、そのペンキでバケツの表面を塗ることはできません。

しかし、よく考えると、バケツがペンキでいっぱいになっているということは、バケツの内側はペンキで塗られているのと同じなのでは……？

それなら表面も塗れてしまうのでは……？

一体どういうことでしょう？