続・同様に確からしい
富山本部校高校部
前回、弦の長さに関する確率の問題を出しました。
3つの考え方で解いてみます。
考え方1
円周上の2点を無作為に選ぶと弦が1つ定まります。
その2点の一方に正三角形の1つの頂点が重なるように回転して考えます。
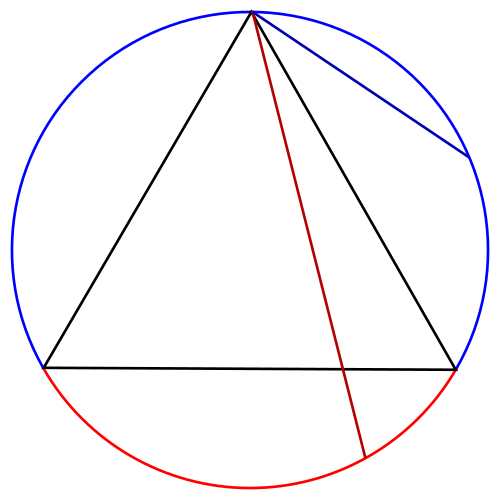
2点のもう一方の位置を考えると、弧の長さの比から確率は 1/3 となります。
考え方2
円の半径を無作為に選び、さらにその上の1点を無作為に選ぶと、その点を通り半径に垂直な弦が1つ定まります。
その半径に正三角形の1つの辺が垂直になるように回転して考えます。
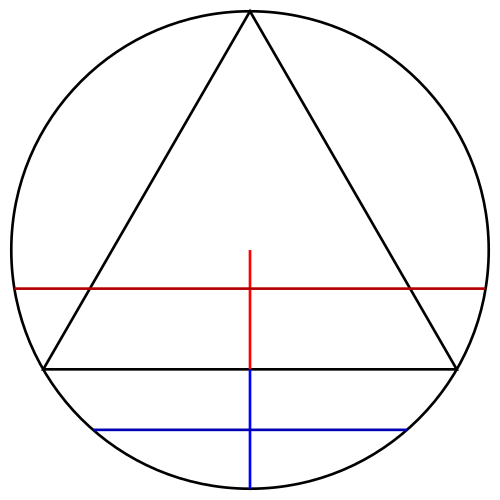
選ぶ1点の位置を考えると、線分の長さの比から確率は 1/2 となります。
考え方3
円の内部の1点を無作為に選ぶと、その点を中点とする弦が1つ定まります。
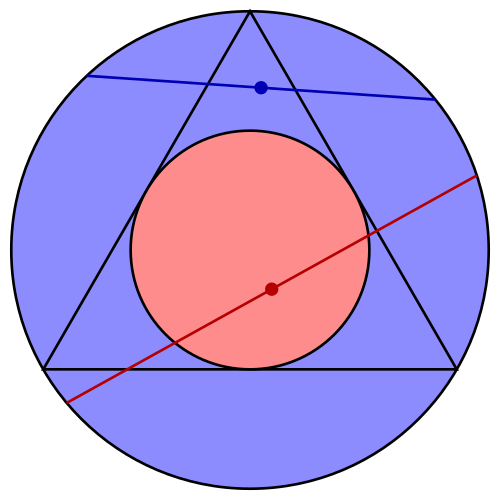
選ぶ1点の位置を考えると、面積の比から確率は 1/4 となります。
……全てバラバラの結果になってしまいました。
それぞれの考え方に間違いはなさそうに見えますが……。
なぜこのようなことになったのでしょう。
